G. Vantongerloo
Réflexions sur l'existence absolue des choses
Fin.

Le cercle inscrit et le cercle circonscrit d'une ellipse déterminent les points sur elle.

La perpendiculaire sur l'axe des x, menée par un point sur le cercle principal et le point formant l'intersection avec la dite perpendiculaire et la ligne parallèle à l'axe des x, passant par le point formé par le rayon du cercle directeur, allant vers le point donné du cercle principal, indique le point correspondant de l'ellipse. Il en résulte également qu'un poids est plus lourd aux pôles qu'à l'équateur. D'autre part, tout tend vers l'équateur et celà encore par la rotation. Si par exemple, une ellipse a comme valeur du grand axe 10, et 8 pour le petit axe, quel est le degré du point M de l'ellipse?

Lorsque le point M sur le cercle inscrit et le cercle circonscrit de l'ellipse considérée aura 30^o, le point M occupera sur l'ellipse:

Par rapport au centre, le point M aura 24^o 37' 30?

Par rapport au foyer F' le point M aura 13^o 30' 10?

Par rapport au foyer F le point M aura 80^o 39' 40?

Si un poids, à n'importe quel lieu de la terre, se trouvait toujours au centre de la terre, le poids serait invariable. Or la terre étant une ellipse a deux foyers qui eux font varier le poids suivant le degré du point M par rapport aux foyers.

On peut remarquer que le point M tend vers l'équateur et échappe constamment du cercle inscrit, tandis que lorsque le point M approche les pôles, son poids écrase le cercle de plus en plus, ce qui démontre la raison pour laquelle un poids est plus lourd aux pôles qu'à l'équateur.

Si deux corps s'attirent en raison directe de leurs masses et en raison inverse du carré de leur distance, il y a lieu de tenir compte de la vitesse de chaque corps. La raison inverse du carré de leur distance, sauve en partie la raison de la vitesse, vitesse des corps dont je crois qu'il faut tenir compte

La force attractive est relative à la vitesse des corps.

La vitesse d'un corps augmente suivant que l'on s'approche du corps en mouvement comme elle diminue suivant que l'on s'en éloigne. C'est la vitesse apparente. Mais la vitesse acquise existe. On ne peut plus dire de deux corps de masse égale et de vitesse différente qu'ils s'attirent en raison directe de leurs masses et en raison inverse du carré de leur distance. La vitesse est une facteur que l'on ne peut négliger. D'autre part, si deux corps de masse différente ont une vitesse égale pour une raison attractive ou répulsive, causée par une troisième masse et ensuite par rapport à cette masse, la thèse de l'attraction universelle n'est plus vraie. Il est vrai que la vitesse de ces deux corps se trouverait changée si leur distance venait à se modifier. Mais il est aussi vrai que la distance de deux corps se trouverait changée si leur vitesse se modifiait. On ne peut jamais, d'une manière absolue, déterminer l'attraction universelle, puisque le nombre des facteurs à introduire va à l'infini Il y a par exemple la forme de la masse, relative à son centre ou à ses foyers, ce qui forme une attraction différente C'est que sur le systême référent terre, l'attraction varie suivant le lieu et un poids est plus lourd aux pôles qu'à l'équateur. Celà tient, comme nous avons déjà dit, aux foyers de la terre et est relatif au lieu que l'on occupe par rapport à ces foyers qui eux différent de la vitesse de la rotation. Si les poids diffèrent, ce n'est pas par la force attractive, mais par la vitesse de la terre même, qui lui donne la forme d'un éllipsoïde ce qui est une conséquence de la vitesse.

La loi attractive dérive donc purement de la vitesse et dire que le centre de la terre attire, c'est négliger de dire que la vitesse forme ce centre. Les corps s'attirent donc par rapport à la vitesse des autres corps qui sont cause de la vitesse des corps entre eux. Tout cela se tient.

Dès que nous ne sommes pas fixés sur la terre (rivés dessus) nous oscillons entre les foyers et le centre de l'ellipse de la terre et si nous tombons (la chute des corps) elle est due à cette oscillation mais pas à l'attraction de la terre. D'ailleurs la terre ne nous attire pas mais elle nous aspire par sa rotation. Donc elle nous écrase contre elle et cet écrasement est relatif à la position que nous occupons sur la terre par rapport à ses foyers et son centre. Nous cherchons constamment à tomber. Nous oscillons vers un équilibre qui se rompt à chaque pas car nous ne pouvons jamais être en équillibre parfait avec trois choses à la fois, les foyers et le centre. L'oscillation du pendule est ainsi justifiée. On sait que le pendule simple, qui bat la seconde, est plus court à l'équateur qu'aux pôles. Donc les oscillations entre les foyers qui sont plus distantes lorsqu'on se trouve aux pôles sont plus lentes et, plus courtes, lorsqu'on se trouve à l'équateur où les foyers sont en ligne droite. Evidemment la différence n'est pas énorme vu que les foyers de la terre sont relativement très près du centre.

La ligne droite est celle qui est également située entre ses extrémités.

Suivant Archimède, la ligne droite est la ligne la plus courte entre deux points.

L'espace n'est pas géométrique et je suis sûr qu'Euclide en était aussi conscient que ceux qui prétendent à une géométrie non-euclidienne. Euclide savait fort bien que sa définition de la droite n'était pas exacte d'un façon absolue et immuable car une courbe peut très bien être située entre ses extrémités. La définition d'Euclide ne prête pas à équivoque et un jeu de mots viendrait mal à propos. Euclide devait aussi bien savoir que sa géométrie n'était qu'un moyen et que la nature ne contient pas la géométrie qui n'est qu'un produit du cerveau. A priori, l'homme crée une géométrie pour déterminer certains points qu'il dit être dans l'espace. Avant, arrière, à gauche, à droite, haut et bas, sont déjà les premières notions géométriques. Les points dans l'espace se présentent à priori objectivement à nos sens et pour les déterminer il nous faut un moyen. Par conséquent, la géométrie euclidienne est la seule et tout indiquée pour déterminer les choses d'une manière utile. Il n'est d'ailleurs pas possible d'établir une géométrie non-euclidienne sans avoir recours à la géométrie euclidienne. La géométrie non-euclidienne dit que la somme des trois angles d'un triangle n'est pas égale à deux droites, mais pour les calculer il faut qu'elle ait recours à la géométrie euclidienne. Deux angles droits n'existent pas dans une géométrie non-euclidienne.

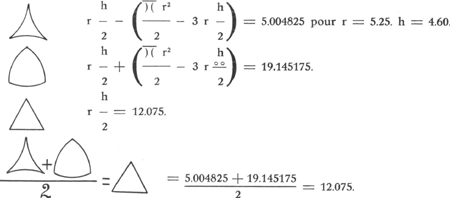
Ainsi, la droite d'Euclide est bien définie car la somme de la superficie d'un triangle convexe et concave, divisée par deux, est égale à un triangle dont la somme est égale à deux droites.

La géométrie euclidienne est encore approuvée par les observations de Helmholtz et Lobatschefski. Je reproduis leurs réflextions d'après Elie De Cyon (Dieu et Science): Ainsi Helmholtz reconnaît ‘que tous les systèmes pratiques de mesuration géométrique où les trois angles de grands triangles réctilignes ont été mesuré isolément, notamment tous les systèmes de mesurations astronomiques, qui donnent une valeur égale à zéro aux parallaxes des étoiles fixes éloignées,....confirme empiriquement l'axiome des parallèles et montre que, dans notre espace et avec nos méthodes de mesuration, la mesure courbure ne diffère pas de zéro.’ En ceci Helmholtz est d'accord avec les affirmations de Lobatschefski: ‘J'ai trouvé ailleurs, écrit ce dernier, en m'appuyant sur quelques observations astronomiques que, dans un triangle dont les côtés sont de la même grandeur à peu près que la distance de la terre au soleil, la somme d'angle ne peut jamais différer de celle de deux angles droits d'une quantité qui puisse surpasser 0.0003 en secondes sexagésimales. Or, cette différence doit êatre d'autant moindre que les côtés du triangle sont plus petits’. Cette quantité minime ne dépasse d'ailleurs pas les limites des erreurs d'observation.

Une démonstration peut être dite ‘avoir une valeur’ lorsque les hypothèses et les démonstrations répondent à: savoir donner une explication suivant les faits incontestablement établis et par conséquent, ne pas contredire ou aller à l'encontre de ces faits de sorte que la démonstration en est facile.

Si je dis, le temps absolu, je dis un mot vide de sens, car le temps absolu n'existe pas. S'il existait, nous aurions une unité de mesure et nous n'avons trouvé encore que la durée prise comme temps. Personne ne peut donner une définition du temps et cela parce qu'il est inexistant. Si je prends la rotation de la terre comme unité de mesure, j'ai, par un système de division, une mesure de durée et ma nouvelle coordonnée aura pour T, un nombre donné, d'heures, minutes, secondes ou des fractions. Ce qui veut dire, une durée. Et, si je prends comme unité de mesure la vitesse de la lumière, T, ne sera pas encore le temps absolu, mais une nouvelle durée, prise comme unité. Mais comment vais-je subdiviser cette nouvelle unité? Si je la divise en 300.000 Km à la seconde, j'aurais combiné une unité de mesure (seconde) avec une nouvelle unité et ma division n'a pas de sens, pas plus que le mot espace. Je puis très bien mesurer un objet mais jamais que par rapport à un autre objet et cela avec un moyen (soit le mètre) qui n'a une raison d'être que pour fixer les idées. Si je vois par exemple un mur isolé de tout objet, si possible, je puis mesurer sa hauteur, sa largeur et son épaisseur en prenant comme coordonnées la base et l'extrèmité du mur. Mais imaginons-nous un mur sans fin. Il fait par exemple le tour de la terre et il a une hauteur au delà de nos moyens de perceptibilité. C'est à dire, il va à l'infini. Que serait notre moyen de mesure? Nous ne pourrions jamais définir que la distance qui nous sépare ou que sépare un objet du mur et par conséquent, une mesure d'espace devient impossible.

Le mot ESPACE-TEMPS est une convention qui a l'utilité de fixer les idées et de faciliter certaines opérations algébriques en introduisant des inconnus qui auront une valeur conventionnelle, soit des mètres, secondes, longueur d'ondes, vitesse, etc....qui eux mêmes sont conventionnels et nous servent pour fixer les idées.

Je vois un phénomêne de la nature. Pour le constater, j'ai besoin d'en déterminer certains faits dans un temps donné à un moment donné. Si je n'ai pas de moyen de mesure, je n'ai pas de point de comparaison. De même pour évaluer sa situation dans l'espace, c'est-à-dire à une distance de, par rapport à, j'ai toujours besoin d'une unité de mesure.

Mais ai-je par là déterminé l'espace et le temps et puis-je prendre une chose qui a servi pour fixer les idées pour une chose absolue. Si le mot dimension signifie impor-

tance, alors nous sommes en droit d'appeler la mesure, que nous avons pris dans l'idée, temps, comme 4 ème dimension. Mais en géometrie le mot dimension se rattache particulièrement à la mesure de la distance et la mesure d'une durée au mot temps. Il est vrai qu'une distance peut avoir une durée, mais ici une 5 ème dimension s'introduit. C'est une durée, multipliée par la vitesse. La distance de Paris à Lyon est de 512 Km. quel est le temps qu'il faut pour faire cette distance. Ici, le temps est fonction de la vitesse, car, si on fait cette distance à pied, en chemin de fer, ou en aéroplane, la distance aura changé ainsi que le temps. Tout cela veut dire qu'il n'y a rien d'absolu et d'immuable et, pour la nature de choses, c'est très heureux car sinon, l'infini serait fini et tout serait à l'encontre de la continuité.

Nous devons nous arrêter à la capacité de nos sens. Au delà et en deçà nous ne pouvons rien percevoir et nous rentrons dans les suppositions vagues et imaginaires. Nos moyens de mesuration nous suffisent amplement pour comprendre ce qui est compréhensible par l'homme. Comme tout est mortel, ne cherchons pas l'absolu. Lorsqu'une idée est bien coordonnée avec nos moyens de mesurations et de réflexions, nous pouvons l'admettre. Mais, qu'avancerait le monde si je lui dis que la terre a pris un mouvement accéléré de X fois la durée de nos 24 heures et que son accélération entraîne tous les faits observables. C'est à dire, que si la terre tourne 4 fois plus vite, nos montres prendront une vitesse proportionelle à la nouvelle vitesse de la terre ainsi que tout évènement de la terre. Nul n'est capable, ni dans le présent, ni dans le passé, ni dans le futur, de dire que pareil fait ne s'est pas produit ou ne se produira pas puisque tout se transforme en même temps et proportionnellement. Où allons-nous donc fixer, comme valeur absolue, le mot TEMPS et ESPACE.

Je puis très bien construire une géométrie non-euclidienne, non-lobatschefskienne, non-riemanienne et je ne dis pas que ces géométries n'ont pas de raisonnement. Je dis même que toutes ont une certaine importance et peuvent être utilisées, mais aucune n'est capable de prouver l'existence absolue du TEMPS et de L'ESPACE.

125 tours à la seconde fait une dynamo. Sur un disque, mis en mouvement par la dynamo, se trouve un carré à 6 centimètres du centre du disque. Lorsque le disque fait un tour, le carré aura parcouru une distance de 34.557.521.200 centimètres.

Lorsqu'un point immobile à la vue de l'homme, prend une vitesse (celle de la dynamo par ex.) 125 tours à la sec. ce même point qui parcourt 4.219.680 mètres à la sec. aura disparu. Mais par rapport à un appareil photographique lorsque celui-ci déclanche à une vitesse de 1/10 de sec. ce même point laissera une traînée circulaire. Le point apparait allongé. Donc: la vitesse et le repos n'existe que par rapport à un spectateur et suivant que son système (appelons le système de référence) soit dans la condition nécessaire, soit pour voir le mobile en repos ou en mouvement. On pourra classer ce phénomêne dans l'optique car ce ne sont que des phénomènes apparents et qui n'ont pas une existence réelle.

Deux points en mouvement par rapport au sens de la vue de l'homme, tendent à se raprocher et ils se combinent pour ne former plus qu'un, lorsque leurs mouvements s'accélèrent à une vitesse telle que celle de 125 tours à la sec. Une barre en mouvement se difforme, même tous les objets sont vus par l'homme sous un autre aspect que la forme réelle. Nous ne pouvons juger d'un objet, ni de son mouvement ou de son repos, ni de sa forme, même pas de son existence réelle. Tout est en mouvement et le mouvement transforme. Le mouvement existe par rapport à d'autres mouvements, ou encore mieux, par rapport aux mouvements entre eux. Ces mouvements sont pris pour être au repos, lorsque le système, pour les percevoir, est dans les conditions voulues, ce qui veut dire, conditions de vitesse nécessaire.

Tout cela correspond donc bien à un segment de l'infini qui devient fini lorsque les rapports forment un, sans relation des deux rapports. C'est à dire 8/8 = 1, rien n'est visible.

Si nous percevons certains phénomènes, c'est que notre sens est dans les conditions de vitesse nécessaires. Je ne parle même pas de l'angle ou de l'aspect que prend le phénomène lorsqu'il est perçu par notre sens, car le phénomène semble varier de sens à sens.

Tout ceci explique que la théorie de Lorentz n'est qu'un fait optique et que la contraction semble exister, mais n'existe pas en réalité.166

Je dis donc, qu'un point matériel en mouvement au delà d'une certaine vitesse de notre sens, disparaît. Mais d'autre part, la vitesse de la lumière est de 300.000 Km. à la sec. A cette vitesse, un point matériel à disparu à nos sens. Et pourtant, nous constatons l'existence de la lumière. Je dis, nous constatons car la lumière se dévoile à la surface qu'elle occupe. Les points matériels, les phénomènes, deviennent visibles par notre sens par la lumière qui les dévoile. Mais la lumière, nous ne la voyons pas, mais bien les surfaces qu'elle occupe ou qu'elle éclaire et lorsque ces surfaces ont un rapport ou sont dans la condition nécessaire avec la vitesse de notre sens, nous les percevons par la lumière qui les dévoile. La lumière peut donc avoir une vitesse de 300.000 Km. à la sec. peu importe puisque nos sens ne perçoivent pas la lumière mais bien les surfaces qu'elle occupe.

Nous ne pouvons donc pas fixer une unité de mesure ou de comparaison et par conséquent nous ne pouvons rien définir d'une façon absolue et tout ce que nous pouvons dire, c'est que les choses qui semblent exister, n'existent que par rapport à une relation de vitesse. Relation entre l'objet ou le phénomène et notre sens de perceptibilité. Mais puisque la lumière est la condition primordiale et indispensable pour donner jour aux rapports de ces deux relations, nous pouvons dire avec Einstein, que la lumière est notre point d'appui pour déterminer l'espace et le temps.

Les choses sont visibles par intermédiaire de la lumière à condition que leurs vitesses dans les mouvements universels, soit en rapport avec la vitesse de nos sens. Ce rapport est la seule condition pour que la lumière soit à même de les rendre perceptibles à un spectateur. Donc la lumière n'est pas relative, mais, suivant une vitesse d'un object, relative à d'autres vitesses et relative à la vitesse de nos sens, la lumière nous permet de constater. Nous ne pouvons que constater, mais sans la lumière, les rapports ne peuvent être constatés. Mais lorsqu'une chose se manifeste à nos sens, nous ne pouvons pas pour cela déterminer l'existence de cette chose. Les faits optiques, les contractions, nous empêchent de pouvoir déterminer la forme d'un objet. Rien n'est vrai que dans certaines conditions. D'autres conditions rendent le problème invraisemblable et même insoluble.

FOTO: COUSEMÜLLER

FOTO: COUSEMÜLLER